Data for Meta-analysis Need to be Prepared a Certain Way – Here’s How

Data for meta-analysis need to be assembled into a dataset before you can import it into statistical software and start your analytic work. This post will show you how to prepare your dataframe for meta-analysis in the package rmeta for R.

Data for Meta-analysis Are Challenging Because of the Underlying Scientific Literature

The most important point I want to make is that if you bring me a dataset and ask me to analyze it for a meta-analysis, I’m going to sit you down and start interrogating you. You will feel like a criminal accused of a felony! It’s a harrowing process. Here is what I am going to ask you:

• Are you sure you found absolutely all the academic papers with a study on your topic? If so, show me the evidence.
• Are you sure you applied the inclusion and exclusion criteria properly? If so, show me the evidence.
• Are you sure the articles that qualified and made it into your meta-analysis have the exact right numbers reported in them to fairly include in our analysis? If so, show me.
• Are you sure there are not a bunch of other meta-analyses on this subject? Because if there are, then you really are in trouble, because you didn’t do your homework before contacting me!

All of this is not because I want to play professor and quiz you to death (although I admit that can be fun!). It’s because we will have to write about all this in the methods section of any peer-reviewed article we write, so we might as well get this stuff out of the way immediately when we first meet.

The Most Common Problem with Meta-Analysis

The most common problem with trying to prepare data for meta-analysis is that when you try, you find you actually can’t do a meta-analysis the way you had planned. The reason why you can’t do one is either that there are no studies on your topic in the literature, or else, the studies that are there are so badly designed you can’t use them.

I like to tell this joke. My joke goes like this: Every Cochrane Collaboration report ends with the same generic finding: “We narrowed our search down to four, semi-crappy studies, so we can’t make any recommendations. Please, if any scientists out there are reading this, for the love of God, do some quality studies so we can say something next time we do this!”

Preparing Data for Meta-Analysis in Package rmeta

Assuming you get over all the scientific literature and study design hurdles and are actually able to narrow your articles down to a handful (I had 15 in a systematic review I did), you are ready to extract the data from them. I’m going to come up with a simple scenario, and demonstrate an outcome that is a percentage, as is done on this example from rdrr.io.

Scenario for Meta-Analysis

Let’s use Disney characters for this one. Imagine in 2007, Goofy has a philosophical difference with Minnie Mouse and Daisy Duck, who are all researching what flavor of ice cream is most likely to induce happiness. Goofy believes that vanilla should always be used as the control flavor, and Minnie and Daisy believe that it depends on the situation. Therefore, they part ways, and Goofy founds his research institute dedicated to ice cream and happiness research: the Goofy Institute.

Here is the timeline of the literature:

• In 2008, unrelated team Bugs Bunny and Daffy Duck conduct lab studies suggesting that chocolate flavor increases risk of happiness.
• Minnie and Daisy jump on this finding. In 2008, they complete a clinical trial (of which Minnie is the head) on about 300 participants. They randomize them to either chocolate (treatment) or vanilla (control) and measure happiness as an outcome (yes/no).
• Findings are weak and mixed, so Minnie and Daisy obtain funding for a much bigger study led by Daisy in 2012, including about 1,000 participants (about 500 in each treatment group). Again, chocolate is the treatment, vanilla is control, and results are inconclusive.
• During this time, the Goofy Institute, located in New England, had been chasing the “Berry hypothesis”. Most of the testing done there had been on strawberry-flavored ice cream, but now that Goofy’s old colleagues were getting findings, he contacted them. They decided to do a multicenter study on chocolate.
• In 2015, the Goofy Institute underwrote a multi-center study of chocolate vs. vanilla ice cream in terms of rates of happiness. Daisy and Minnie were collaborators, and over four sites, they enrolled around 2,000 participants.

I put all the data and code from this project on Github.

Data Dictionary

Below is a screen shot of our data dictionary.

This dictionary represents a minimum dataset needed to run the meta-analysis.

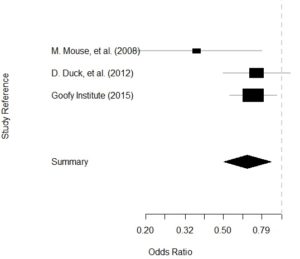
• Name: This is a character string representing the article. In our example dataset, you will see I put the first author followed by the year. This is the field you imagine printing out on the left side along the y-axis of the Forrest plot.
• Trt_Denom: This stands for “treatment denominator”. This is the number of participants in the treatment group – so in our scenario, the number of participants randomized to chocolate. Notice that we are including those enrolled in the study in the chocolate group – not necessarily those finishing the study. It is possible to have “death by chocolate” during the study – as evidence, a local restaurant had that on the dessert menu. So, we have to do an intent-to-treat analysis.
• Cnt_Denom: As you probably guessed, this stands for “control denominator”. This would be the number of participants enrolled and randomized to vanilla, philosophical issues with calling vanilla “control” aside. Just a reminder – you can die from too much vanilla ice cream as well!
• Trt_Num: This stands for “treatment numerator”. This is the number of people in the treatment group – the chocolate group – that got the outcome (got happy). Another way of saying it is it’s the number of people reported in the Trt_Denom field that actually got the outcome – so if you put Trt_Num over Trt_Denom in a fraction, you get the rate of the outcome in the treatment group.
• Cnt_Num: This stands for “control numerator”, and as you probably guessed, this is the number of people in the control group – vanilla – who got the outcome – happy. Again, this has to be a number smaller than or equal to Cnt_Denom, because this is the rate of the outcome in the control group.

Data Entry

When I do the data entry into the spreadsheet, I like to put the articles in order of publication. That way, I can see any trends over time in the Forrest plot. Also, make sure that you designate the numeric fields as integer with no decimals or commas, so that R reads them in as numeric.

I usually do data entry into an *.xlsx, and then, I save that as a *.csv to read into R. Here is a screen shot of our *.xlsx:

What’s interesting about these data is that you never really see the total number of people in the study – it’s just the denominator for each group. Another thing you have to contend with is that in real life, you don’t just gather one outcome – you gather many. In fact, the example data I linked you to from rdrr.io included two outcomes.

Two outcomes essentially mean two different numerators. Let’s say that our team also asked about whether the ice cream made the participant sleepy (as well as happy). Then rates of sleepy would be in their own Forrest Plot. We’d have to have two sets of columns for the data (e.g., Trt_Num_Happy, Cnt_Num_Happy, Trt_Num_Sleepy, and Cnt_Num_Sleepy). We could use the same dataset for each Forrest plot, we’d just have to make sure we were calling up the right fields in our analysis.

Running the Plot

The whole point of preparing data for meta-analysis is running the plot! And luckily, if you prepare the data properly, running the plot is straightforward. I will place the code here.

Let’s examine this code:

• As you can see, we start by reading in the *.csv of the data I showed you above into a dataset called goofy.
• Next, we call the rmeta package.
• After that, we make an object called calc which has our calculations in it. As you can see, we use the command meta.DSL. In the argument, we list all of our numeric columns, set our data to goofy, and set the names that will be used in the plot as our Name variable.
• Then we run a summary of the calc. I didn’t show you the output, but if you run it, you will see that it reports the odds ratios (ORs) for each article based on the data we gave it (which is essentially a 2 x 2 table), with 95% confidence intervals.
• Finally, we plot the calc object and get our Forrest plot.

Plot is below:

Updated July 30, 2021. Spaghetti junction photograph by JimmyGuano. Added video on September 13, 2021. Reformatted code and added video slider April 3, 2022.